The golden rectangle is the basis for many forms in nature, and has been used in architecture for thousands of years. It is also called the “golden section,” and the ratio between its width and height is called the “golden ratio” or “golden mean.”
There are many geometric objects that can be made from this special rectangle, including the icosahedron that we’ll make in this project. An icosahedron is made of twenty identical equilateral (all sides equal) triangles. It sounds complicated, but it’s easy to make by starting with just one golden rectangle, then making two rotated copies of it.
And once that object is complete, we can remove the triangles to uncover a star-studded surprise.
We’ll use SketchUp for this project – a free and fun program for 3D modeling. You can use SketchUp to design just about anything, from furniture to a dream bedroom to an entire city. The free, web-based version of SketchUp can be found online here
When you start modeling in SketchUp, you start in this view, with Helen standing on the ground. She isn’t needed in this model, so press E for the Eraser, and click on any of Helen’s edges.

Make sure you can see the origin – the point where the red, green, and blue axes meet. This is where we’ll center the first rectangle.
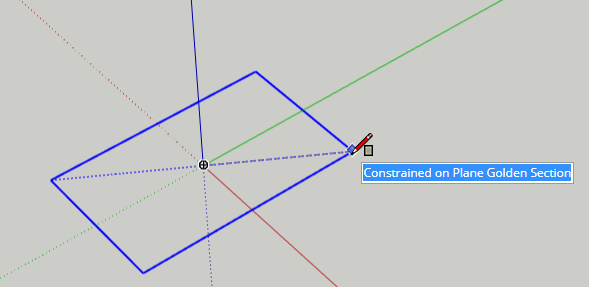
Press the R key for the Rectangle tool. The rectangle needs to be centered on the origin, so before clicking anywhere, tap (don’t hold) the Ctrl key (PC) or Option key (Mac). Then tap (don’t hold) the Up arrow so that the rectangle will be in the red-green plane.
Click the origin to start, then move the mouse and click when you see the Golden Section popup.
We need two copies of this rectangle, each oriented in a different plane. To keep these rectangles from sticking to each other, we’ll make the first one into a group. Press the Spacebar for the Select tool, and double-click on the rectangle – this selects the faces plus all four edges.
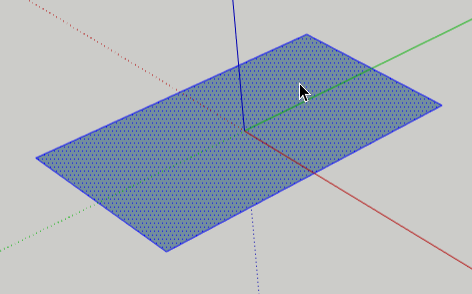
Right-click on the rectangle, and choose Make Group.
After the group is created, keep it selected (highlighted).
Now we’ll make the first rotated copy. The steps for rotating several times can seem a bit complicated, so read carefully!
Press Q for the Rotate tool, and click to place the protractor at the origin.
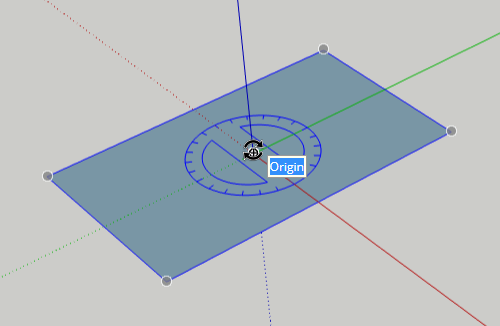
Making a rotated copy requires two more clicks. First, tap the Ctrl key (PC) or Option key (Mac) which means a copy will be made.
Click anywhere away from the origin to set the first rotation point. Then move the mouse to spin the rectangle around, stopping when you see 90 degrees in the Angle field at the lower right. If you can’t get 90 to appear, just type 90 and press Enter. (Don’t click in the Angle field, just type.)
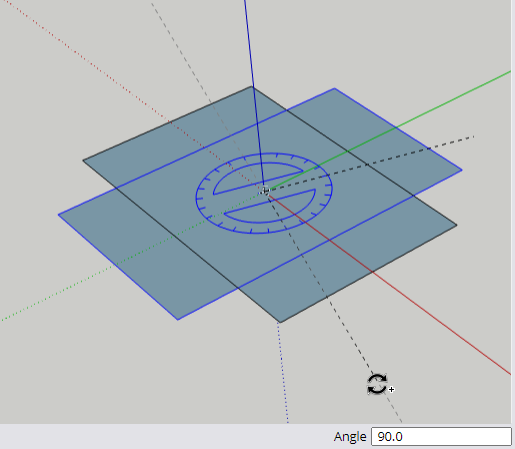
Keep the copied rectangle selected, and the Rotate tool should still be active. The rotation this time will be in another direction. Tap the Right arrow which turns the protractor red. This means the protractor is locked in the green-blue plane. Like before, click to place the protractor at the origin.
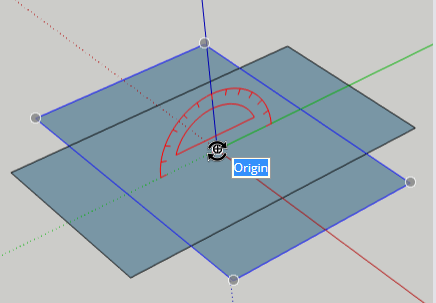
This time we’re not making a copy, just rotating what’s selected. Click anywhere to start the rotation, and click again when the angle is 90 degrees. The second rectangle is now in the right place.
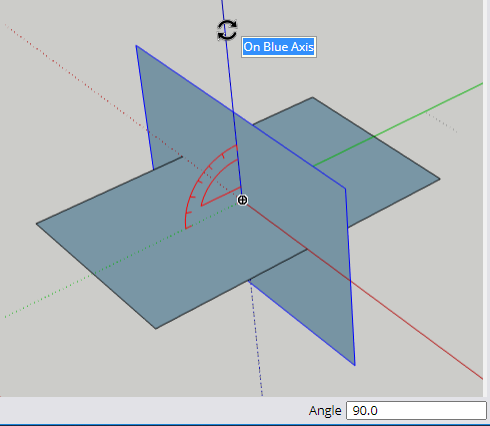
One more copy to go! With the second rectangle still selected, and Rotate still active, tap the Left arrow to turn the protractor green, and place it at the origin.
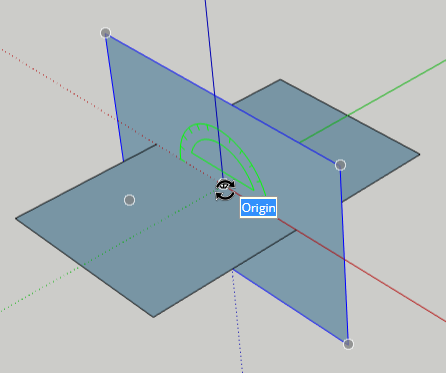
Tap the Ctrl / Option key and use two clicks to make a 90-degree copy.
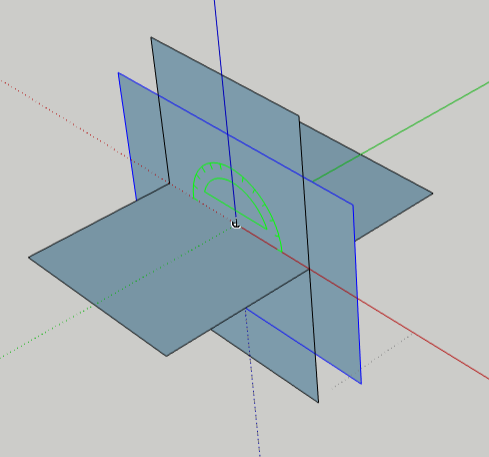
To rotate this new rectangle, tap the Up arrow for a blue protractor, and place it – where else? – at the origin.
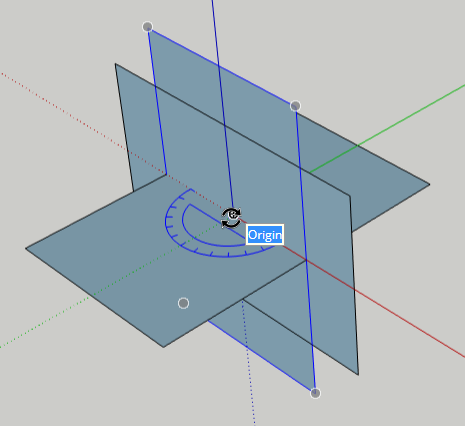
Spin this one around 90 degrees.
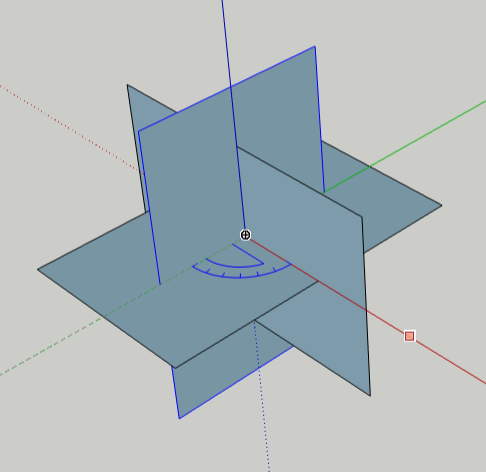
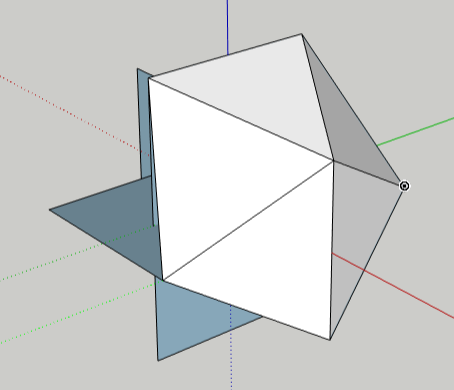
The rectangles don’t need to be groups anymore. So select them all by pressing Ctrl+A (Cmd+A on the Mac), then right-click on any rectangle and choose Explode.
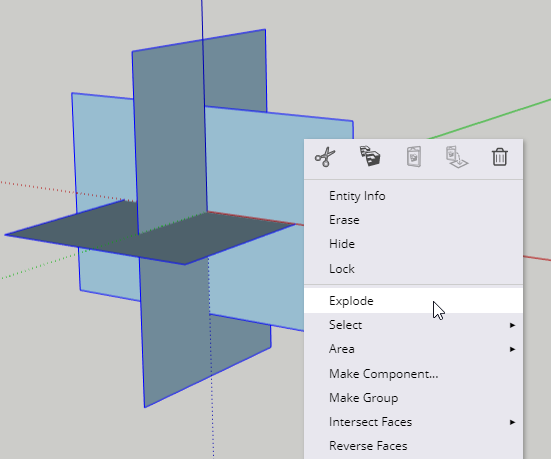
This leaves all three rectangles selected.
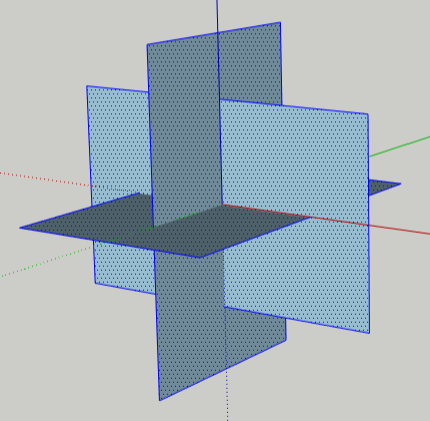
Right-click anywhere in blank space to unselect them.
Now we have all the geometry we need, and we can create the triangular faces of the icosahedron. Press L for the Line tool, which draws edges. Draw lines between any three adjacent corners, to complete the first triangle. You don’t need to draw a line where an edge already exists, such as between Point 1 and Point 3 below.
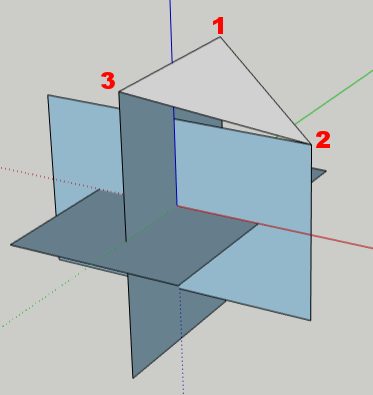
After completing the first triangle, the rest are easy. Here’s one place you can create the second triangle:
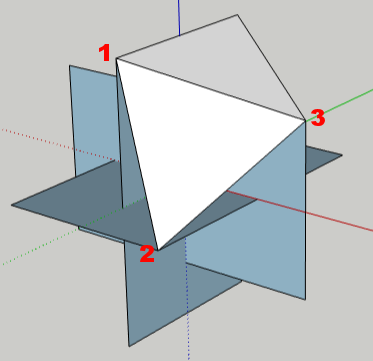
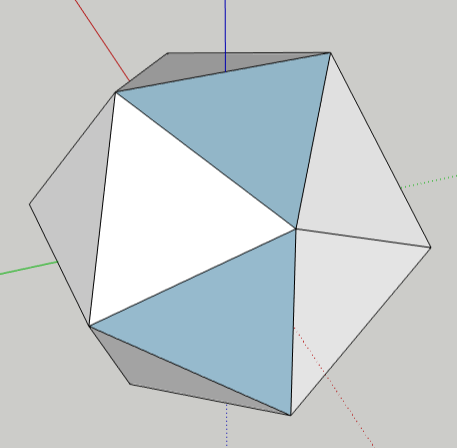
Keep going until your first five triangles surround one point. In the end, all corners will have five triangles around them
As you add more lines, extra lines are also being created inside the icosahedron. These lines will become edges of the cool shape we’ll uncover at the end.
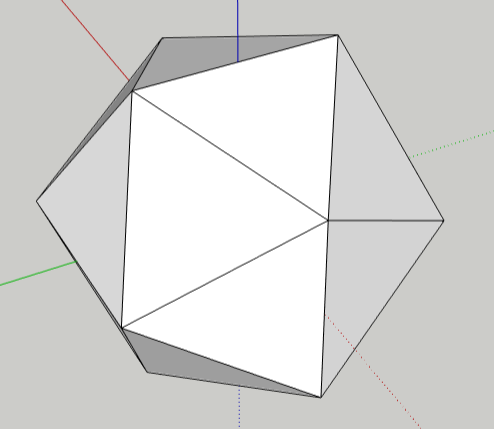
When all lines have been drawn, you’ll have a set of 20 triangles. Some triangles might be gray – this is SketchUp’s “back face” color.
You can switch a face’s front and back colors by right-clicking on the face and
choosing Reverse Faces.
The easiest way to make sure there are 20 triangles is to count them while painting them. To open the colors, click the Materials icon along the right side, then click the Magnifying Glass icon at the top and open the Colors folder.
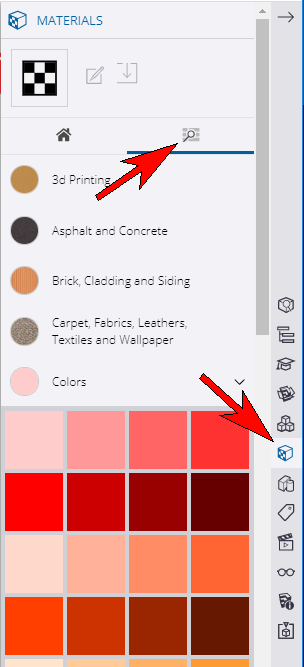
Click a color, then click each triangle to paint it, counting each one until you get to 20.
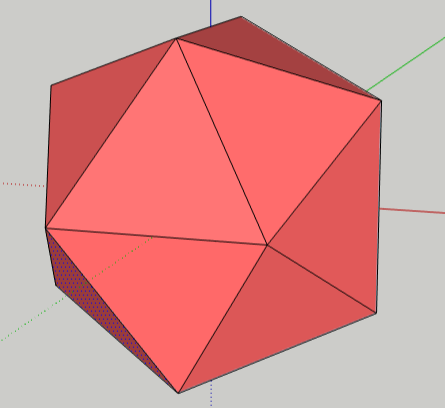
Now for some coloring challenges.
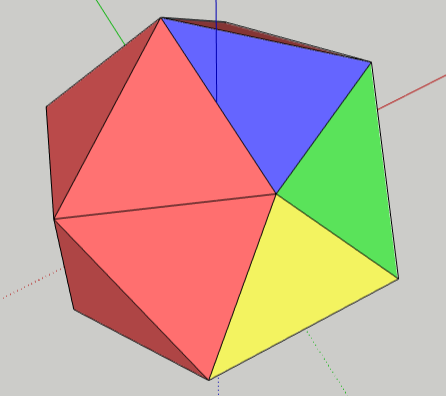
First, we’ll try to paint faces so that no two adjacent triangles will have the same color. This is actually pretty easy – it can be done with only four colors. Start by picking three more colors and painting the triangles around one point.
Back in the Materials window, click the House icon to see the colors used so far. The extra ones are from Helen, who was erased at the very beginning.
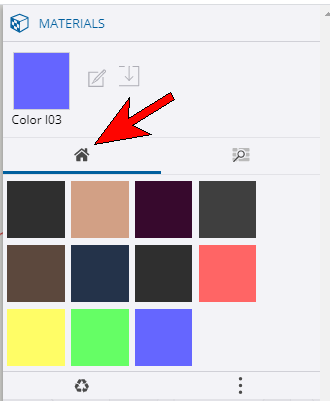
Get the triangle-painting colors from here, so that you don’t have to search for the same yellow or green each time.
Paint the rest of the triangles using the same four colors, making sure that no triangles of the same color are next to one another.
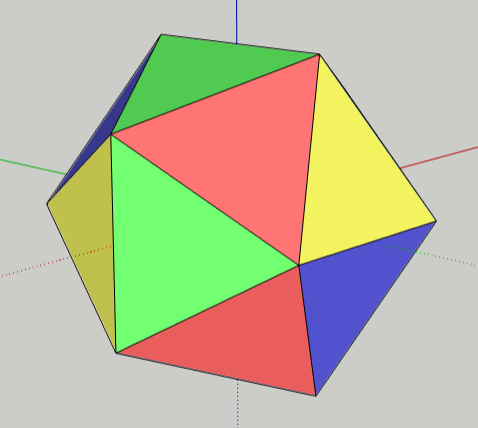
(Cool fact: No matter what object you’re painting, in 2D or 3D, you can always paint it using just four colors, and keep faces from touching. This is why most maps use four colors.)
Now let’s try a harder painting problem – using no repeating colors around any point. This means that the five triangles that meet at any point will each have a different color, so you’ll need five colors. It’s harder than it looks, and you’ll probably have to repaint a lot of triangles.
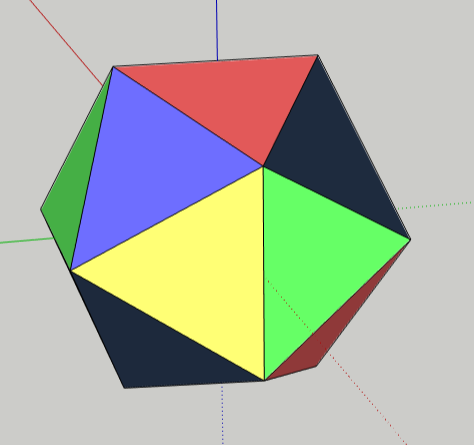
Now let’s see what’s happening beneath the triangles.
We could remove each of the 20 triangles one at a time, but there’s a faster way. Activate Select (Spacebar) and keep the Shift key pressed, which lets you select more than one face at a time. Select one triangle of each color (five triangles total).
Then right-click on any selected triangle and choose Select / All with same material.
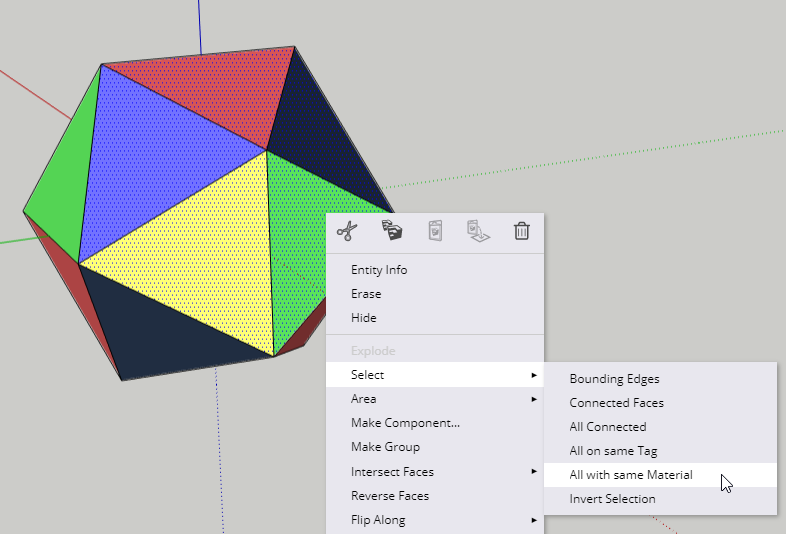
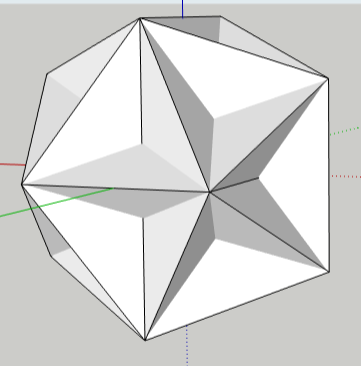
This selects all 20 triangles. Press the Delete key to erase the faces all at once. This is what you uncover: 12 faces that each have a 3D five-pointed star on them.
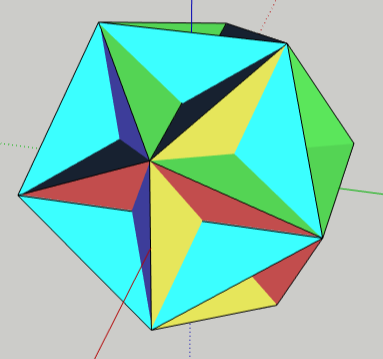
Color challenge for this star object: use just six colors and make sure no color is repeated at any point. It’s really tough!
Learn More
Golden Ratio Definition
https://en.wikipedia.org/wiki/Golden_ratio
What is the Golden Ratio
https://www.mathsisfun.com/numbers/golden-ratio.html
Golden Ratio in Design
https://blog.prototypr.io/golden-ratio-what-it-is-and-why-should-you-use-it-in-design-7c3f43bcf98
Nature and the Golden Ratio
https://www.mathsisfun.com/numbers/nature-golden-ratio-fibonacci.html