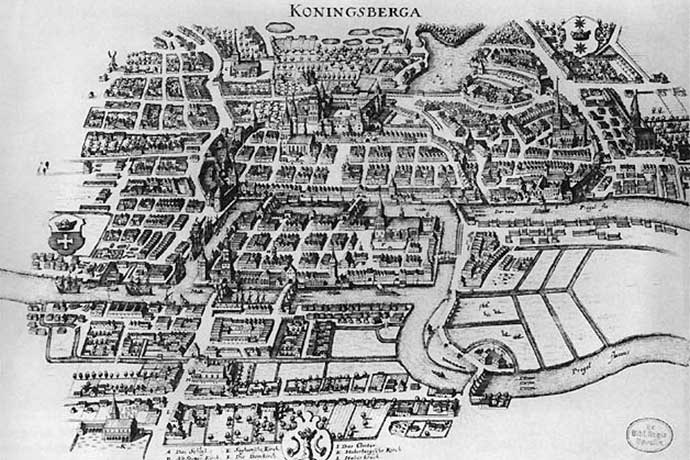
The puzzle is called The Seven Bridges of Königsberg. It’s based on an actual city, then in Prussia, now Kaliningrad in Russia. The city is divided by a river with two islands in between and, further downstream, the river splits the city again.
The problem is deceptively simple: there are (or were, in Euler’s time) seven bridges to connect the two islands and the downstream parts of the town. Euler wondered if a person could walk across each of the seven bridges once and only once to touch every part of the town. Starting and ending at the same spot was not a requirement.
Here is a map you can use to try and solve the problem for yourself:
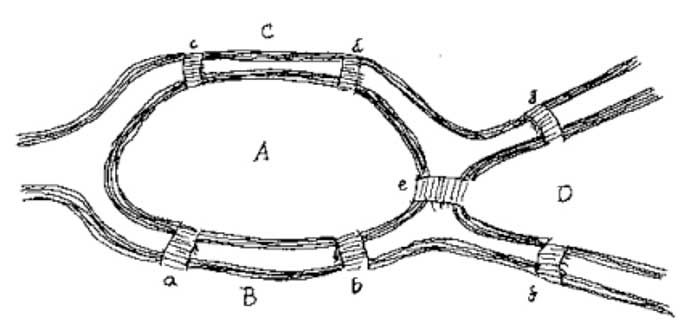
Which do you think is more important to solve this problem: the number of bridges or the location of each bridge?
Answer: the number of bridges.
Euler proved the number of bridges must be an even number, for example, six bridges instead of seven, if you want to walk over each bridge once and travel to each part of Königsberg. The solution views each bridge as an endpoint, a vertex in mathematical terms, and the connections between each bridge (vertex). Euler realized only an even number of bridges yielded the correct result of being able to touch every part of the town without crossing a bridge twice.
Euler used math to prove it was impossible to cross all seven bridges only once and visit every part of Königsberg. By doing so, he set in motion a series of discoveries and insights about how space and intersecting spaces can be defined, as well as their properties. A detailed description of Euler’s solution in in the Wikipedia link below this article.
If you’ve ever seen a mobius strip, for example, you've seen an example of topology, a mathematical field of study evolved from Euler’s solution to this problem. Topology is concerned with space and how things connect one to another, as well as continuity and boundaries of space. Topology also studies how properties of a space change and don’t change when the space is expanded or contracted.
In computing, topology is useful in understanding the networks (paths) data can flow within any system, as well as how sets of data might relate to each other. The Seven Bridges of Königsberg also is similar to another common computing problem called sometimes the Traveling Salesman Problem where you try to find the most efficient route given a set of restrictions like the seven bridges in Euler's problem.
Non-mathematicians (likely you, definitely me) experience the Traveling Salesman problem any time we get on a train or bus. The Traveling Salesman Problem is figuring out the most efficient way to travel between pairs of cities of specified distances. Managing scarce resources (trains, buses) that travel along finite routes is a perfect problem for computing to solve because computers are faster and more efficient. But first we need Euler and others to state the problem and define solutions with math. We then program our computers to do the math.
Topology also deals with set theory, how groups of things can be sorted into sets to identify common elements with other groups as well as unique elements. A Venn diagram is a great example of a set. And programming sometimes has to sort data in different ways. Which sorting method works best for a situation can be determined by set theory.
And what happened to the seven bridges from Euler's time? Two did not survive World War II. Two bridges were demolished and replaced with a single highway. Of the three remaining bridges, one was rebuilt in 1935 while the other two remain intact as Euler knew them. And, of course, Königsberg, Prussia has changed its name to Kaliningrad, Russia.
Learn More
The Seven Bridges of Königsberg
http://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg
http://mathforum.org/isaac/problems/bridges1.html
http://www.contracosta.edu/legacycontent/math/konig.htm
Topology Helps Map the Human Brain
http://www.nonlinearbiomedphys.com/content/1/1/3